あいさつ

最近 PixInsight を導入して使い始めました．このソフトには ArcsinhStretch というストレッチ機能があり，結局どういうことをやっているのか少し気になったので調べてみました．

「色を保つ」とは

よく ArcsinhStretch では色が保持されるといいます．これはどういうことでしょうか．
まずは普通のストレッチを考えてみましょう．普通は次のようなアルゴリズムでストレッチをします．
変換前を$$r, g, b$$，変換後を$$R, G, B$$とおきましょう．

$$R = f(r), G = f(g), B = f(b)$$
$$
f(x) = \begin{cases}
0 & (x < m) \
\frac{F(x - m)}{F(M - m)} & (m \le x \le M) \
1 & (x > M)
\end{cases}
$$

関数$$F$$は通常$$\log$$や√，線形関数などがありますが，色が保持されるとは，変換後の$$R, G, B$$の比率が変換前の$$r, g, b$$と変わらないことを言います．
このことは，色相と彩度が変わらないということです．これらを式で見てみると，
$$Max = \max(R, G, B), Min = \min(R, G, B)$$
$$H = \begin{cases}
60 * ((G - B) / (Max - Min)) ,; \max(R, G, B) = R \
60 * ((B - R) / (Max - Min)) + 120 ,; \max(R, G, B) = G \
60 * ((R - G) / (Max - Min)) + 240 ,; \max(R, G, B) = B
\end{cases}
$$
$$S = (Max - Min) / Max$$
であることから，たとえば，$$R’ = k \cdot R, G’ = k \cdot G, B’ = k \cdot B (k > 0)$$であるような変換であれば，三色の値の大小関係も保たれ（最大値は$$Max’ = k \cdot Max$$，最小値は$$Min’ = k \cdot Min$$），色相と彩度が基本的に保たれる，つまり色が保たれるということになります．
$$H: \frac{60 * (G’ - B’)}{Max’ - Min’} = \frac{60 * (k \cdot G - k \cdot B)}{k \cdot Max - k \cdot Min} = \frac{60 * (G - B)}{Max - Min}$$
（上の式については他のケースについても同様）
$$S: \frac{Max’ - Min’}{Max’} = \frac{k \cdot Max - k \cdot Min}{k \cdot Max} = \frac{Max - Min}{Max}$$
この$$k$$（ストレッチファクターとも呼びます）を決めるときに，Arcsinh関数を使うことで，ArcsinhStretchが実現できます．したがって，（自分は勘違いしていたのですが）Arcsinh関数を使うことと色が保持されることは特に関係はありません．
どの画素に対しても$$R, G, B$$に対して同じ$$k$$を掛け算するようなストレッチ方法であれば，必ず色は保持されます．

The key point is that to preserve color the calculated pixel multiplier must be simultaneously applied to all channels (R,G,B) in the pixel.
ArcsinhStretch― by Mark Shelley

どう計算するか

実際に$$k$$を決めるのは，次のような式で決めます．
$$L = \mathrm{Luminance}(R, G, B)$$
$$k = \frac{\mathrm{arcsinh}(\beta \cdot L)}{L \cdot \mathrm{arcsinh}(\beta)}$$
画素ごとにストレッチファクターを一意に決めるため，輝度の値を使っています．前述したように，上の式の Arcsinh 関数は，別に他の関数でも問題ありません．実際，PixInsight でも他の関数でもできるようにしたいという Future Work が書かれています．
輝度―$$k$$のグラフを書くと，こんな感じの概形になります．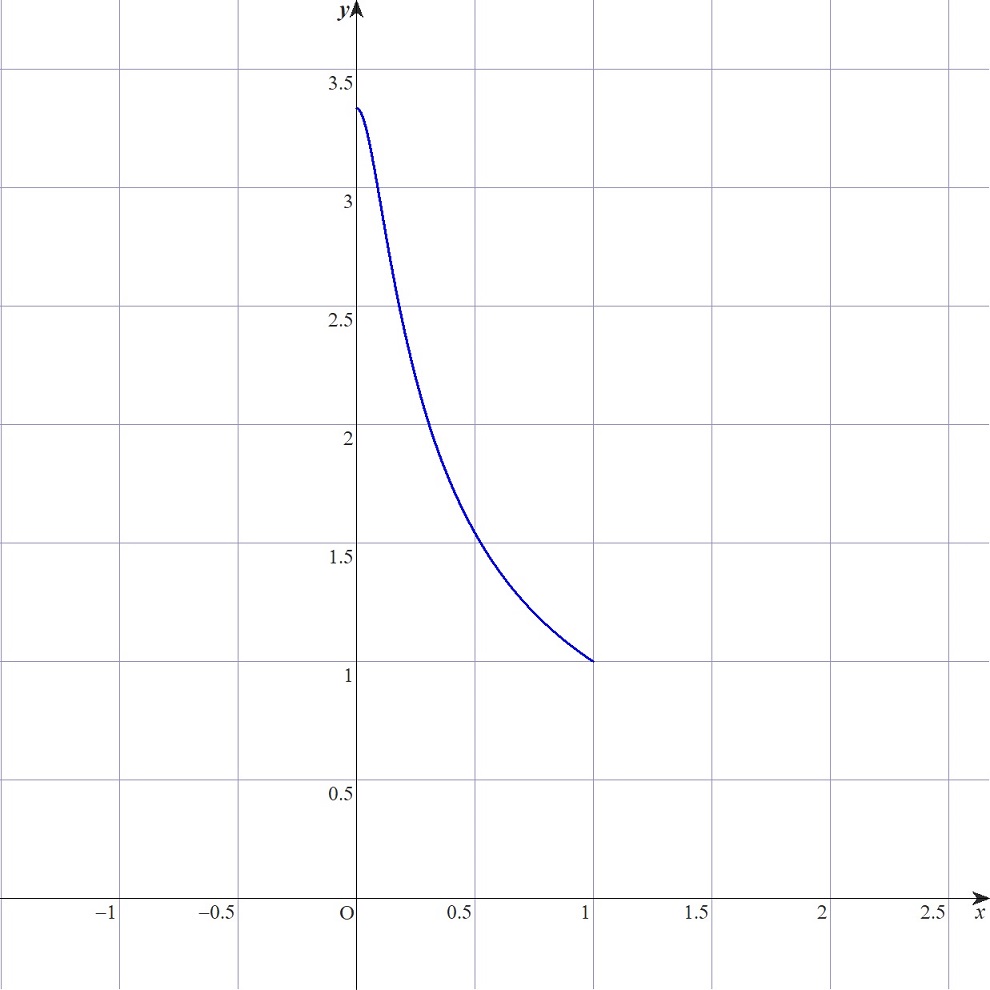
輝度―kのグラフ
上では$$\beta = 10$$としてみました．この値が大きくなればなるほど，$$x = 0$$での値も大きくなるように変化します．この値は$$\frac{\beta}{\mathrm{arcsinh}(\beta)}$$となるようです．
暗い画素ほどより大きい値で，明るい画素ほど$$1$$に近い値でスケーリングされます．これにより，明るい星まわりの階調をなるべく保存しつつ，暗い部分を持ち上げていることになりますね．
直観的な操作を提供するため，PixInsight では0から1000までの値で$$k$$の最大値（上のグラフで言うところの$$x = 0$$での値だと思われます）をユーザ入力としています．

実際に実装してみる

上の$$k$$を決める式を$$\beta$$について解く方法は少なくとも僕にはわかりませんでしたので，とりあえず$$\beta$$をユーザ入力とするような ArcsinhStretch を実装してみたいと思います．
コードはこんな感じ…．

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
extern crate libm;
/*省略*/
fn run_apply_arcsinh_stretch(
    image: &WcsArray,
    beta: f32,
) -> Result<IOValue, IOErr> {
    dim_is!(image, 3)?;
    let image = image.scalar();
    let mut out = image.clone();
    for (j, slice) in image.axis_iter(Axis(1)).enumerate() {
        for (i, data) in slice.axis_iter(Axis(1)).enumerate() {
            //R, G, B値は予め[0, 1]の範囲で正規化されているものとする
            //画素の輝度値を求める．
            let l = (data[0] + data[1] + data[2]) / 3.0;
            //画素のk（ストレッチファクター）の値を決める
            let s_fact = libm::asinh((l * beta) as f64) / (l as f64 * libm::asinh(beta as f64));
            let s_fact = s_fact as f32;
            
            out[[0, j, i]] = s_fact * data[0];
            out[[1, j, i]] = s_fact * data[1];
            out[[2, j, i]] = s_fact * data[2];
        }
    }
    Ok(IOValue::Image(WcsArray::from_array(Dimensioned::new(
        out,
        Unit::None,
    ))))
}

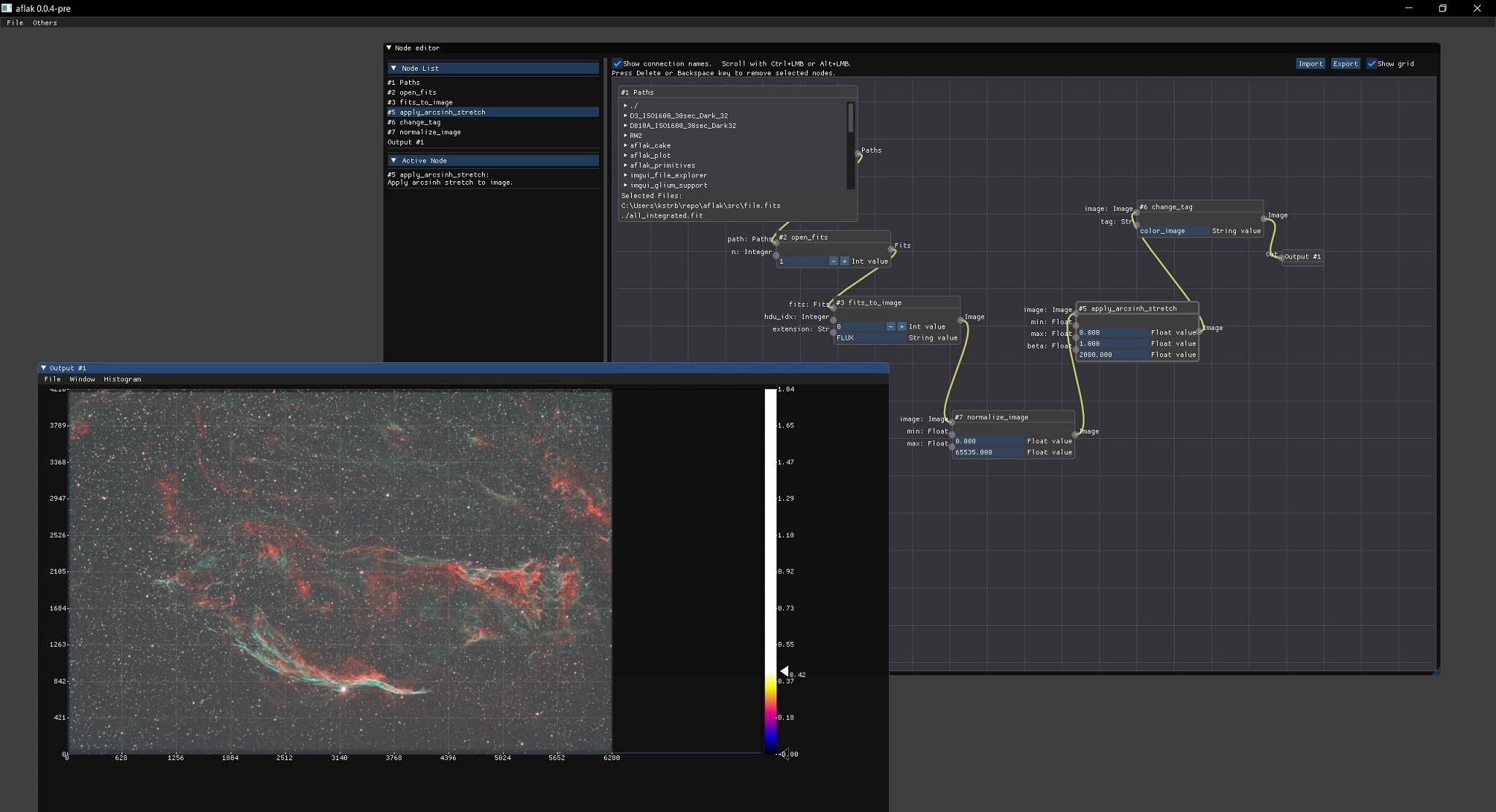それっぽいそれっぽく持ち上がっています．

いかがでしたでしょうか？まとめると

  • 色を保つような変換の一つとして，画素の各RGBを同じ値だけ定数倍するような変換がある．この値は画素ごとに違う分には当然問題ない．
  • この定数として輝度の Arcsinh（をスケーリングしたもの）を利用すると，ArcsinhStretch を実現できる．
  • 必ずしも Arcsinh を利用しなければ色を保てないわけではない．logやsqrtを利用しても何か面白い結果が得られるかも．

ということがわかりました．arcsinh 以外の関数でストレッチした場合にどうなるかも見ていきたいと思いますが，今回のところはこれまで．
それでは．